[Compiler Construction in Ocaml] Hindley-Milner Type Inference System Implementation

I want to spend some time talking about implementing Hindley-Milner type inference system in Ocaml for a ML-ish langauge. The code is available at my Github, under ps6/mlish_type_check.ml.

PeterYaoNYU/CompilerInOCaml

A compiler for a C-ish language, implemeted in OCaml

OCaml 0

This is part of the project for NYU graduate level capstone course by Prof. Joseph Tassarotti.

AST for ML

Before delving into the implementation of the type inference system, let me first provide you with the AST for the ML-ish language that we are doing type inference on:

type var = string   (* program variables *)
type tvar = string  (* type variables *)
type pos = int

type tipe = 
  Tvar_t of tvar
| Int_t
| Bool_t
| Unit_t
| Fn_t of tipe * tipe
| Pair_t of tipe * tipe
| List_t of tipe
| Guess_t of tipe option ref

type tipe_scheme = Forall of (tvar list) * tipe

type prim = 
  Int of int
| Bool of bool
| Unit   (* unit value -- () *)
| Plus   (* add two ints *)
| Minus  (* subtract two ints *)
| Times  (* multiply two ints *)
| Div    (* divide two ints *)
| Eq     (* compare two ints for equality *)
| Lt     (* compare two ints for inequality *)
| Pair   (* create a pair from two values *)
| Fst    (* fetch the 1st component of a pair *)
| Snd    (* fetch the 2nd component of a pair *)
| Nil    (* the empty list *)
| Cons   (* create a list from two values *)
| IsNil  (* determine whether a list is Nil *)
| Hd     (* fetch the head of a list *)
| Tl     (* fetch the tail of a list *)

type rexp = 
  Var of var
| PrimApp of prim * exp list
| Fn of var * exp
| App of exp * exp
| If of exp * exp * exp
| Let of var * exp * exp
and exp = rexp * pos

It is not too complicated, but the type inference system is indeed complicated.

Recursive Type Check Function

Here is the main entrance of the type inference program:

let rec tc (env: (var * tipe_scheme) list) (e: exp) =
  (* print_endline (expr2string e);  *)
  match e with 
  | Var x, _ -> instantiate (lookup env x)
  | PrimApp (prim, exp_list), _ -> 
    (match prim, exp_list with
    | Int int, [] -> Int_t
    | Bool bool, [] -> Bool_t
    | Unit, [] -> Unit_t
    | Plus, [e1; e2]
    | Minus, [e1; e2]
    | Times, [e1; e2] ->
        let t1 = tc env e1 in
        (* print_tipe t1; *)
        let t2 = tc env e2 in
        if (unify t1 Int_t) && (unify t2 Int_t) then Int_t else type_error "Arithmetic operation failed"
    | Eq, [e1; e2] -> 
        let t1 = tc env e1 in
        let t2 = tc env e2 in
        if (unify t1 Int_t) && (unify t2 Int_t) then Bool_t else type_error "Equality operation failed"
    | Lt, [e1; e2] -> 
        let t1 = tc env e1 in
        let t2 = tc env e2 in
        if (unify t1 Int_t) && (unify t2 Int_t) then Bool_t else type_error "Less than operation failed"
    | Fst, [e1] ->
      let t1 = tc env e1 in
      (* print_tipe t1; *)
      (
        match t1 with
          | Pair_t (t, _) -> 
            t
          | Guess_t r -> 
            (
              match !r with
              | Some Pair_t (t1, t2) -> t1
              | None ->
                (* print_endline "In Fst guess"; *)
                let g1 = guess() in
                let g2 = guess() in
                r:= Some (Pair_t (g1, g2));
                (* print_endline "return g1 in Fst guess"; *)
                g1
              | _ -> type_error "Fst applied to non-pair, fail in guess"
            )
          | _ -> type_error "Fst applied to non-pair"
      )
    | Snd, [e1] ->
      let t1 = tc env e1 in
        (
          match t1 with
            | Pair_t (_, t) -> t
            | Guess_t r -> 
              (
              match !r with
                | Some Pair_t (t1, t2) -> t2
                | None ->
                  (* print_endline "In Snd guess"; *)
                  let g1 = guess() in
                  let g2 = guess() in
                  r:= Some (Pair_t (g1, g2));
                  g2
                | _ -> type_error "Snd applied to non-pair, fail in guess"
              )
            | _ -> type_error "Snd applied to non-pair"
        )
    | Cons, [e1; e2] ->
      let t1 = tc env e1 in
      let t2 = tc env e2 in
      (
        match t2 with
        | List_t t -> if unify t1 t then List_t t else type_error "Cons type mismatch"
        | Guess_t _ -> List_t t1
        | _ -> type_error "Cons applied to non-list"
      )
    | Pair, [e1; e2] ->
      let t1 = tc env e1 in
      let t2 = tc env e2 in
      Pair_t (t1, t2)
    | Nil, [] -> 
      let g = guess() in List_t g
    | IsNil, [e1] ->
      let t1 = tc env e1 in
      (
        match t1 with
        | List_t _ -> Bool_t
        | Guess_t _ -> unify t1 (List_t (guess())) ; Bool_t
        | _ -> type_error "IsNil applied to non-list"
      )
    | Hd, [e1] ->
        let t1 = tc env e1 in
        (match t1 with
        | List_t t -> t
        | Guess_t r -> 
          (
            match !r with
              | Some List_t t'-> t' 
              | Some t' -> t'
              | None -> 
                let g = guess() in
                if unify t1 (List_t g) then g else type_error "Hd guess failed"
          )
        | _ -> type_error "Hd applied to non-list")
    | Tl, [e1] ->
        let t1 = tc env e1 in
        (match t1 with
        | List_t _ -> t1
        | Guess_t r -> 
          (
            match !r with
              | Some t' -> t'
              | None ->
                let g = guess() in
                if unify t1 (List_t g) then (List_t g) else type_error "Tl guess failed"
          )
        | _ -> type_error "Tl applied to non-list")
    | _, _ -> type_error "Invalid primitive application")
  | Fn(x, e), _ -> 
    let g = guess() in
    Fn_t (g, tc ((x, Forall([], g))::env) e)
  | App(e1, e2), _ ->
    let t1 = tc env e1 in
    let t2 = tc env e2 in
    let t = guess() in
    if (unify t1 (Fn_t(t2,t))) then t else type_error "App failed"
  | Let(x, e1, e2), _ ->
    let s = generalize env (tc env e1) in 
    (* print_endline "finish generalize"; *)
    tc ((x, s)::env) e2 
  | If (e1, e2, e3), _ ->
    let t1 = tc env e1 in
    let t2 = tc env e2 in
    let t3 = tc env e3 in
    if (unify t1 Bool_t) && (unify t2 t3) then t2 else type_error "If failed"

This is pretty basic, it is just doing pattern matching for the ast, and recursively call the typecheck program.

There are several tricky part in the program however, namely Forall, Unify, instantiate and generalize. These are the key functionalities that make up the polymorphism of the Hindley-Milner type system. I will dissect their implementaiton one by one.

Forall

Forall is defined in the ast. It is of this type:

type tipe_scheme = Forall of (tvar list) * tipe

The first part is a list of variables. They are the variables that should be instatiated to fresh guesses when applied as a vairable. The second part is the type after the substitution. Forall only applied to let expression, when we bound something to a variable, but would like to keep the polymorphism. So instantiate will only happen when type checking a variable.

Unify

let rec unify (t1:tipe) (t2:tipe): bool =
  match t1, t2 with
  | Guess_t (r1), _ -> (
      match !r1 with
      | Some a' -> unify a' t2
      | None -> (
          match t2 with
          | Guess_t (r2) -> (
              match !r2 with
              | None -> (if r1 == r2 then true else (r1 := Some t2; true)) (* t2 also a guess None: check address *)
              | Some a' -> unify t1 a'
          )
          | _ -> (if occurs r1 t2 then raise TypeError else (r1 := Some t2; true))
      )
  )
  | _, Guess_t(_) -> unify t2 t1
  | Int_t, Int_t | Bool_t, Bool_t | Unit_t, Unit_t -> true
  | Fn_t (t1a, t1b), Fn_t(t2a, t2b) ->
      (unify t1a t2a) && (unify t1b t2b)
  | Pair_t (t1a, t1b), Pair_t (t2a, t2b) ->
      (unify t1a t2a) && (unify t1b t2b)
  | List_t l1, List_t l2 -> unify l1 l2
  | Tvar_t v1, Tvar_t v2 -> (if v1 = v2 then true else raise TypeError)
  | _, _ -> (raise TypeError)

Unify is very hard to get it working correctly. What it is doing is to resolve guesses. Somewhere during execution, we figure out a reasonable type for a previous guess, and we unify it. It either succeeds or fails. If it fails, then there is a type error, meaning that somewhere in the program the types are not compatible. If it succeeds, then it means the program is potentially legal so far, but we may not always resolve all guesses. A function like fn id: x->x is essentially unresolvable standalone. Our best effort would be saying that it is of type Fn_t(a’ -> a’).

The part that I tripped on is 1. Occurs and 2. Handling the case of 2 Guess_t None types.

Occurs

We do not allow recursive types in the Hindley-Milner type system. I think this slide did a good job explaining why.

The answer to the last question in the slide would be it is an indefinitely long sequence. So we want to avoid that.

let rec occurs (r: tipe option ref) (t:tipe) : bool =
  match t with
  | Guess_t (nr) -> (
      match !nr with
      | Some a' -> (if r == nr then true else occurs r a')
      | None -> r == nr
  )
  | Int_t | Bool_t | Unit_t ->  false
  | Fn_t (t1, t2) | Pair_t (t1, t2) -> (occurs r t1) || (occurs r t2)
  | List_t l -> occurs r l
  | Tvar_t _ -> false

This situation will only happen when the there are two guesses, and one type has part of it another guess, and that somehow these two types are being unified. It will not happen when the two types are both Guess None: we got that covered in unify. So you want to check that for the first Guess, the reference address of its content is not the same as some part of the second t type (a guess wrapped around in t). And we do the type check recursively. This is a little mind bending right? Understanding occurs is hard, knowing when this happens exactly is harder.

Unify 2 Guesses

When I program, there is one test case that I cannot pass, however hard I tried. And it took me the whole afternoon plus evening to locate the cause.

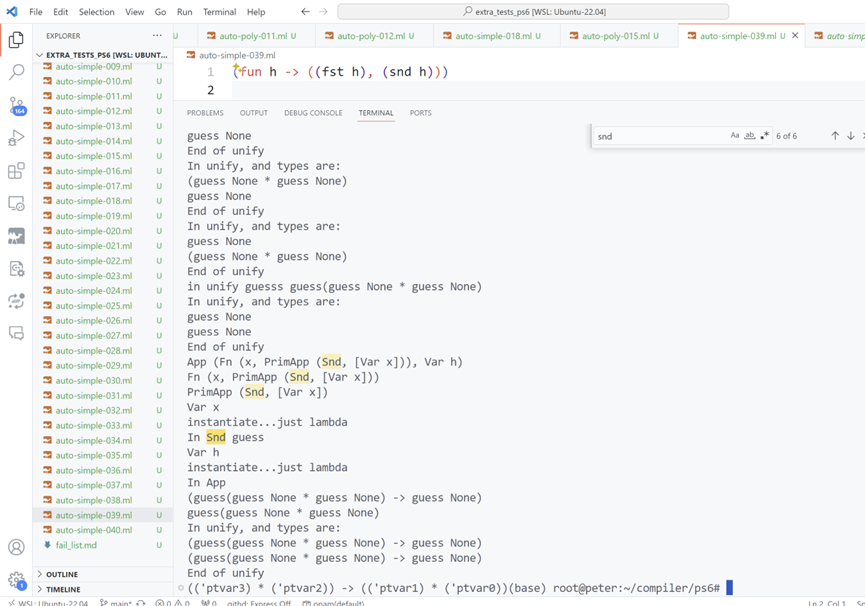
Sorry it is a little blurry. I was taking a screenshot because it was so confusing to me. I forgot exactly how I found the cause of the problem, it was a fleeting moment of human intellectuality. But the problem is that when unifying 2 guess None, I treat them as equal and already unified. What we should do is that, check if their reference point to the same location, and if not, then they are not unified. If there are missing the unify step, then you would have the problem that I encountered, which is that the arguements have type (c * d), while the result has type (a * b). They are not unified properly.

So here is the part of the code where this problem is handled:

let rec unify (t1:tipe) (t2:tipe): bool =
  match t1, t2 with
  | Guess_t (r1), _ -> (
      match !r1 with
      | Some a' -> unify a' t2
      | None -> (
          match t2 with
          | Guess_t (r2) -> (
              match !r2 with
              | None -> (if r1 == r2 then true else (r1 := Some t2; true))
              | Some a' -> unify t1 a'
          )
          | _ -> (if occurs r1 t2 then raise TypeError else (r1 := Some t2; true))
      )
  )

| None -> (if r1 == r2 then true else (r1 := Some t2; true)) This handles the conflict.

Instantiate

The instantiate part is relatively straightforward. It replaces all type variables in the Forall’s list with fresh guesses, so that the polymorphism is achieved. I shall not elaborate on that, since it is easy. (Conceptually easier, but still hard)

Generalize

This part is mind bending!!! How to do generalize, and why we need to eliminate environment bound variables. It is tricky.

let generalize env t =
  let t_gs = guesses_of_type t in
  let env_lists_vars = List.map guesses_constrained_by_env env in
  let env_bound_vars = List.fold_left (fun acc gs -> List.append acc gs) [] env_lists_vars in
  let diff = minus t_gs env_bound_vars in
  let gs_vs = List.map (fun g -> (g, freshvar ())) diff in
  let tc = subst_guess gs_vs t in
  Forall (List.map snd gs_vs, tc)

Guess of types gets out all the guesses in the type t. We want to replace them potentially with variable names (forall constructs), so that when they are encountered later, they can be instantiated with fresh guesses, and hence polymorphic. Implementing it is straightforward, if you are careful enough, unlike me. Just extract all guesses.

let rec guesses_of_type t = match t with
  | Tvar_t x -> []
  | Guess_t r -> 
    begin match !r with
    | Some t' -> guesses_of_type t'
    | None -> 
      (* let new_var = freshvar () in
      r := Some (Tvar_t new_var);  *)
      (* pay attention here, do not return r instead of t *)
      [t]
    end
  | Fn_t (t1, t2) | Pair_t (t1, t2) -> List.append (guesses_of_type t1) (guesses_of_type t2)
  | List_t t' -> guesses_of_type t'
  | Int_t | Bool_t | Unit_t -> []

Next we need to take out the environemnt bound guesses. They should not be generalized. To be in the environment, you have to be in the Let clause, and you have to be a forall construct. You may ask, if they are in a forall structure, then they should already be generalized, and then there should be no bare guesses in the tipe part of the Forall construct. That, my friend, is a deep philosophical question. Think about this situation, where you compile a lambda function. The argument become a Forall([], guess_t ref None) in the env. Then it becomes involved in a Pair, say (fn * 1), and now you need to generalize (Guess_t * this pair). You should not generalize the guess for the lambda argument, because you just can’t: it is not part of a Let clause, and is not intended to be polymorphic. It might later be substituted with concrete Guess ref Some tipe. Later, when the argument finally arrives, the guess of the argument will be resolved. Please do not confuse a function with a function in a let clause, like: let thrd = fun x -> snd (snd x) in thrd (true, (1, (3 :: nil))). Thrd is indeed intended to be polymorphic.

Another good example of why environemnt bound variables should not be generalized is given by Prof. Joseph Tassarotti: \x -> let y = x in y. Without the generalize, we would have x be substituted by a forall construct, which should really be a guess type. Once substituted by a forall, the x will not have relation with the function that is calling it, and has any relation with y.

Well, I kinda have to admit that this is a really weird thing.

So this is the central question of generalize, everything else is conceptually easy. Take the difference of these two sets, replace the guesses with fresh vairables, and returna forall construct. You can check the code yourself.

What an amazing system!